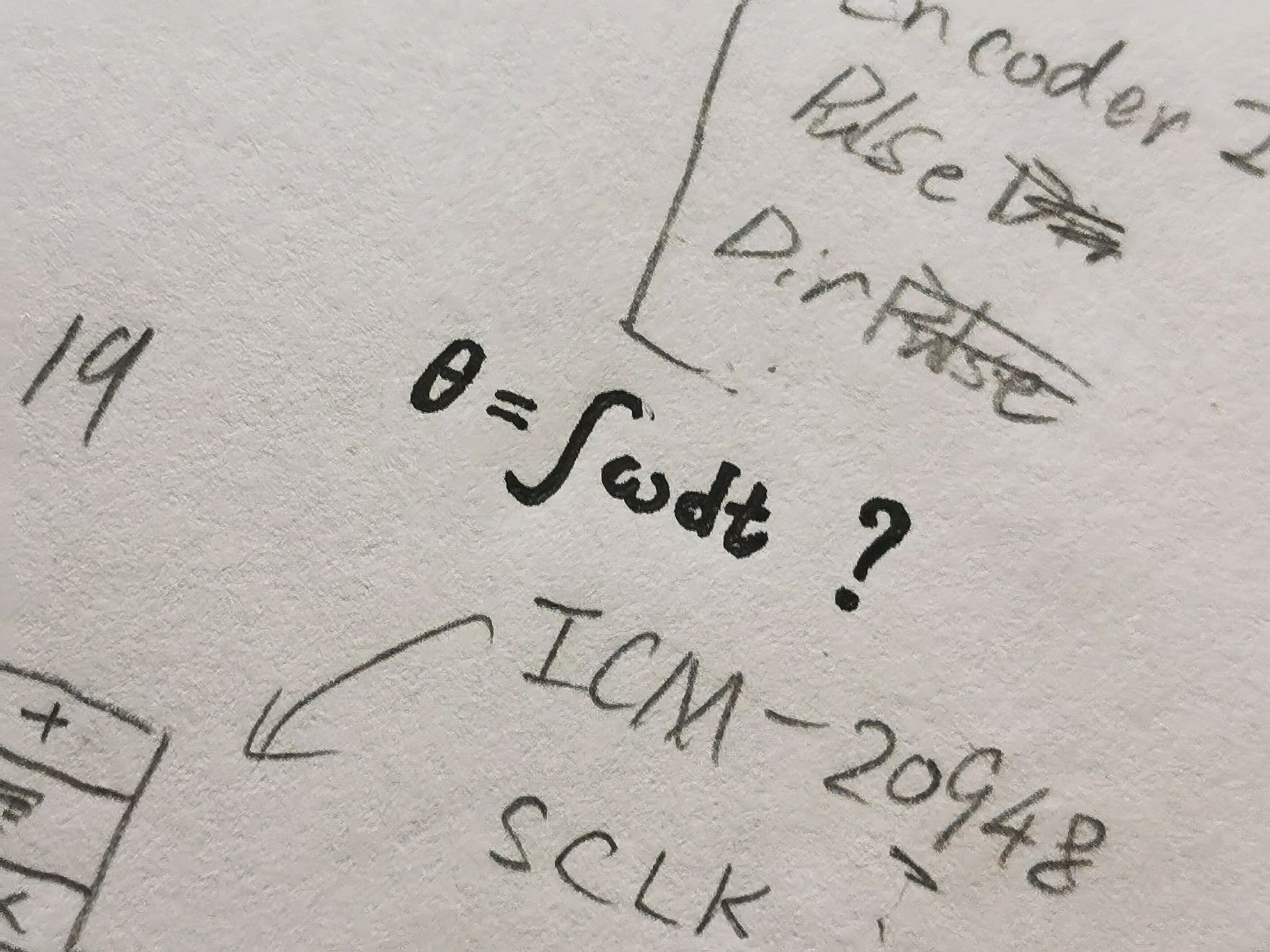在单片机里写出计算小车的俯仰角的代码并不容易。——除非复制粘贴,那轻松多了。
本文的姿态指的是三维空间上的方向姿态. 姿态解算即通过常用的陀螺仪乃至加速度计、磁强计,算出仪器在三维空间中的姿态. 要得到姿态, 那么就必须对手头传感器数据的物理意义有一个初步的认识.
传感器芯片
我常用的是 InvenSense MPU-6050 (数据文档 PDF). 6表示六轴: 三个轴上的加速度, 三个轴上的角速度. 注意, 不是角加速度.
这类的传感器通常称之为惯性测量单元, IMU, Inertial Measurement Unit, 它得名于其基本原理. 这种芯片级的产品又称之为 MEMS IMU, Microelectromechanical Systems, 微机电系统. 人们通过光刻和沉积等工艺在单晶硅表面制造出微小的 (如今普遍是微米尺度) 硅晶体或是金属材质的弹簧、振子、齿轮等一系列机械结构和与之连结的梳状电容器等. 它可以依靠检测电容等参数的改变, 测定机械结构之间的距离, 从而完成机械到电信号的转换. 推荐搜索一下 MEMS 相关的图片直观感受一下.
用于三维姿态解算的主要器件是陀螺仪. 它得到的是载具坐标系下三个坐标轴旋转的角速度, 我们要做的是通过这个角速度算出姿态角.
总体路线
利用陀螺仪, 每隔一段时间$\Delta t$测量一次角速度$\omega$, 即可持续更新当前角度$\theta$:
- $\Delta t$内转过的角度: $\Delta \theta = \omega \Delta t,$
- 等式两边求和得到: $$\theta = \sum_{t=0}^T{\omega_t \Delta t}.$$
当$\Delta t$趋近于无穷小, 可以写成积分形式:
$$
\theta = \int_0^T{\omega(t) \mathrm dt}.
$$
这种连续的公式对于算法, 实现起来没有可行性, 但是很好看. 还是前面的求和比较实在.
这么一来相对于初始朝向的姿态就已经拿到手了. 在二维中, 角度可以简单地像这样直接求和. 这其实就是一般见到的二维海面、路面的航姿推测方法中对角度的处理方法. 我正在计划给二维平面上的姿态解算单独开一篇简单的文章介绍.
但在三维中很难这样做. 如果你是做直立平衡车, 甚至在做无人机, 那么三维空间中的姿态是必不可少的. 需要引入另外的数学工具来解决这个问题: 旋转矩阵, 或称方向余弦矩阵 DCM, Direction Cosine Matrix; 或者一种更加简洁的等价形式, 四元数 Quaternion. 至于为什么三维中直接对角度求和有难度, 其根源是三维中单纯用若干个角度表示一个旋转本身就有困难.
不妨思考一下: 三维旋转怎么用角度表示? 用几个量表示呢? 这几个量有先后关系吗?
下节预告
旋转与其用加法, 不如用乘法. 用乘法表示旋转, 堪称完美.